А. Д. Бендукидзе

 

Золотое сечение

 

Иоганн Кеплер говорил, что геомет­рия владеет двумя сокровищами — теоремой Пифагора и золотым сече­нием. И если первое из этих сокровищ можно сравнить с мерой золота, то второе — с драгоценным камнем.

Теорему Пифагора знает каждый школьник, а что такое золотое сече­ние — далеко не все. Вот мы и ре­шили рассказать читателям об этом драгоценном камне.

 

 

Что  такое  золотое  сечение?

 

Говорят, что точка С производит золотое сечение отрезка АВ, если

АС : АВ = СВ : АС.   (1)

Итак, золотое сечение — это такое деление целого на две неравные части, при котором большая часть так от­носится к целому, как меньшая — к большей. В геометрии золотое сечение называется также делением от­резка в крайнем и среднем отношении. Если длину отрезка АВ обозна­чить через а, а длину отрезка АС — через х, то длина отрезка СВ будет а—х , и пропорция (1) при­мет следующий вид: 

х : а = (а — х) : х   (2)

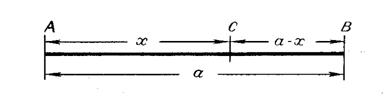
Из   этой   пропорции   видно,   что при золотом сечении длина большего отрезка есть среднее геометрическое, или, как часто говорят, среднее пропорциональное  длин  всего отрезка и его меньшей части:  

Легко сообразить, что верно и об­ратное: если отрезок разбит на два неравных отрезка так, что длина большего отрезка есть среднее гео­метрическое длин всего отрезка и его меньшей части, то мы имеем золотое сечение данного отрезка.

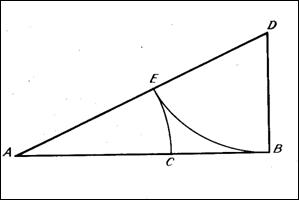Геометрически золотое сечение от­резка АВ можно построить следующим образом: в точке В восставляем перпендикуляр к АВ и на нём откладываем BD = 0,5 АВ; далее, соединив точки А и D, откладываем DE = BD и, наконец, АС = АЕ. Точка С является искомой — она производит золотое сечение отрезка АВ. В самом деле, заметим, что по теореме Пифагора

 

(АЕ + ED)2 = АВ2 + BD2

 

и по построению

 

АЕ = AC,   ED = BD = 0,5 АВ.

Из этих равенств следует, что

 

АС2 + АС· АВ = АВ2,

а отсюда уже легко получается равенство (1).

 

Решая уравнение (2) относительно х, мы находим, что

 

Значит,  Таким образом, части золотого сечения составляют приблизительно 62% и 38 %  всего отрезка.

 

 

Немного истории

 

Древнейшим литературным памят­ником, в котором встречается деле­ние отрезка в отношении золотого сечения, являются «Начала» Евкли­да (III в. до н. э.). Уже во II книге «Начал» Евклид строит золотое се­чение, а в дальнейшем применяет его для построения некоторый пра­вильных многоугольников и много­гранников.

Но золотое сечение было известно и до Евклида. В частности, знали о нем Пифагор и его ученики (VI век до н. э.). В философской школе Пи­фагора помимо философии и матема­тики изучали и гармонию. Занимаясь теорией гармонии, пифагорейцы приш­ли к заключению, что качественные отличия звуков обусловлены коли­чественными различиями между дли­нами струн. Это вдохновило их, и они постарались пойти дальше — вы­разить все закономерности мира через числа, полагая, что в основу мирового порядка бог положил именно число. Поэтому пифагорейцы в числах и их отношениях (а последние рассматри­вались как отношения отрезков) ис­кали магическое, сверхъестественное. И в геометрии не обошлось без мисти­ки. Здесь особо следует отметить любовь пифагорейцев к звёздчатому пятиугольнику, составленному из диа­гоналей правильного пятиугольника. Вот что пишет об этом известный математик и историк математики ван дер Варден в своей превосходной книге «Пробуждающаяся наука»: «Эта фигура, символ здоровья, слу­жила опознавательным знаком для пифагорейцев. Когда на чужбине один из них лежал на смертном одре и не мог заплатить человеку, который уха­живал за ним вплоть до его кончины, то он велел ему изобразить на своём жилище звёздчатый многоугольник; если когда-нибудь мимо пройдёт пи­фагореец, то он не преминет осведо­миться об этом. Действительно, несколько лет спустя один пифагоре­ец увидел этот знак, и хозяин дома получил богатое вознагражде­ние».

Звёздчатый пятиугольник для нас интересен в первую очередь тем, что каждая из пяти линий, составляющих эту фигуру, делит другую в отноше­нии золотого сечения. В самом деле, так как треугольники ACD и ABE подобны, то АС : АВ = AD : АЕ. Но AD = ВС, а АЕ = АС, и поэтому АС : АВ = ВС : АС — уже известная нам пропорция золотого сечения. Именно это свойство звёздчатого пятиугольника и могли использовать пифагорейцы для построения правильного пятиугольника, ибо строить золотое сечение они, безусловно, умели.

К началу эпохи Возрождения усилился   интерес к золотому  сечению.

Он был вызван, в первую очередь, многочисленными применениями золотого сечения как в самой геометрии, так и в искусстве, особенно в архитек­туре. Следствием этого явилось появ­ление книги «Божественная пропорция», автором которой был крупнейший математик XV века итальянец Лука Пачоли. В своем труде Пачоли приводит тринадцать свойств золотого сечения, которое он снабжает такими эпитетами, как «исключительное», «несказанное», «превосходнейшее», «замечательнейшее», «сверхъестест­венное» и так далее. Впрочем, назва­ние книги само говорит об отношении автора к описываемому предмету. Небезынтересно, что иллюстрировал кни­гу один из инициаторов её написа­ния, друг Пачоли, великий Леонардо да Винчи. Между прочим, именно он ввёл сам термин «золотое сечение».

 

 

Лука Пачоли (около 1445 - позже 1509) —

итальянский математик, написав­ший

трактат о золотом сечении

«Божествен­ная пропорция».

 

 

 

Портрет Монны Лизы (Джоконды) был написан Леонардо да Винчи (1452— 1519)гениальным

итальянским худож­ником и ученым эпохи Возрождения. Кар­тина привлекла внимание исследователей, которые обнаружили, что композиция рисун­ка основана на «золотых треугольниках» (точнее, на треугольниках, являющихся кусками правильного звёздчатого пятиуголь­ника).

 

Наблюдения показывают, что с эстетической точки зрения золотое сечение имеет определённые достоинства. Это подтверждается экспери­ментом, который был проведен в кон­це прошлого века: из десяти прямо­угольников, среди которых был и «золотой» (со сторонами, отношение длин которых давало золотое сечение), испытуемый должен был выбрать один. И вот, около 22% общего числа испытуемых выбрало именно «золо­той прямоугольник». Нельзя обойти молчанием и то, что книги, почтовые открытки, бумажники, шоколадные плитки и множество других предме­тов имеют форму золотого прямо­угольника. Отметим здесь же, что если от «золотого» прямоугольника отрезать квадрат или к большей сто­роне «золотого» прямоугольника при­строить квадрат, то получится, сно­ва «золотой» прямоугольник.

Широкое применение находит золотое сечение в архитектуре и ис­кусстве. Множество архитектурных шедевров построено по пропорции золотого сечения. Эта же пропорция лежит в основе многих бессмертных творений Фидия, Тициана, Леонардо да Винчи, Рафаэля.

 

 

Греческий скульптор Леохар (4.в. до н. э.) создал статую Аполлона Бельведерского, воплотившего представления древних греков о мужской красоте. Линии, проведён­ные на снимке, определяют основные пропор­ции тела. Эти пропорции связаны с золотым сечением.

 

Отдали дань золотому сечению также композиторы и поэты. Извест­но, например, что на золотом сечении строил многие свои произведения вы­дающийся венгерский композитор Бела Барток. Что же касается поэтов, то здесь в первую очередь следует назвать гениального грузинского поэта Шота Руставели. Как показали новейшие исследования академика Г. В. Церетели, в основе строения поэмы Ш. Руставели «Витязь в тиг­ровой шкуре» положены симметрия и золотое сечение. В частности, из 1587 строф поэмы больше половины — 863 — построены по пропорции золо­того сечения…

 

 

Отношение золотого сечения

и его замечательные свойства

 

Если в пропорции (2) положить , то относительно  получится следующее уравнение:

   (3)

Положительный корень этого урав­нения равен отношению золотого се­чения:

  

Это поистине замечательное число, обладающее рядом интересных свойств. Вот некоторые из них.

1. Непосредственные вычисления показывают, что

,  

— число, обратное , на единицу больше самого . Легко проверить, что это — единственное положительное число, обладающее таким свойством. В са­мом деле, если положительное z  удовлетворяет соотношению

 

то z должно быть корнем уравнения z2 + z — 1 = 0. Но это уравнение имеет единственный положительный корень: .

 

2. Переписав равенство  (3) в ви­де

 

и   подставив   в   правую часть этого равенства  вместо τ, получим:

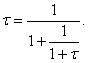
Этот процесс подстановки можно продолжить. В результате мы полу­чим следующее представление числа τ в виде бесконечной цепной дро­би:

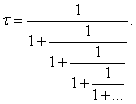   (4)

Нельзя не отметить предельную про­стоту этого представления!

 

3.   Вот  ещё  одно представление числа τ:

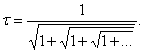   (5)

Чтобы   придать  смысл  равенству (5), изучим последовательность

, , , , … ,

общий член которой (обозначим его через φn) содержит n радикалов.

Непосредственно видно, что {φn} — возрастающая последовательность. Кроме того, она ограничена. В са­мом деле, так как φ1 = 1 < 2 и (φn+1)2 = 1+φn , то из φn < 2 следует, что

φn+1 << 2, и по индукции зак­лючаем, что φn < 2 для любого (на­турального) n.

Итак, {φn} — возрастающая, огра­ниченная последовательность. А как известно, такая последовательность является сходящейся. Обозначив предел последовательности φn через φ, можно написать:

.

 

С  другой   стороны,   переходя   к пределу в равенстве (φn+1)2 = 1 + φn , получим:

Таким образом, (положительное) число φ является корнем квадратно­го уравнения

φ 2 — φ — 1 = 0, а число

— корнем уравнения

,

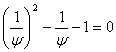или умножая на

,

,

откуда

— получаем равенство (5). И здесь бро­сается в глаза предельная простота представления!

 

 

Приближение числа τ

рациональными числами

 

Представление (4) очень удобно для приближения иррационального числа  рациональными числами. С этой целью обратимся к «подходящим» дробям:

 

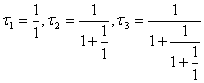
и вообще для любого n

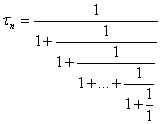    (6)

 

Последовательность этих дробей имеет пределом число , и поэтому каждое  является приближением этого числа. Непосредственные вы­числения показывают, что

 

Этот ряд дробей построен по очень простому закону: числитель каждой дроби равен знаменателю предыду­щей дроби, а знаменатель — сумме числителя и знаменателя той же дроби. А как будет дальше? Сохра­няется ли эта закономерность? Легко доказать, что это так. В самом деле, как видно из формулы (6), со­седние подходящие дроби  и  связаны соотношением

 

и поэтому из равенства

следует, что

 

Этот  простой  закон  образования подходящих дробей числа даёт воз­можность легко выписать их последо­вательность:

 

Из теории цепных дробей извест­но, что подходящие дроби с нечётны­ми номерами убывают и приближают­ся к порождающему эти дроби числу справа, а дроби с чётными номерами возрастают и приближаются к тому же числу слева. Применяя это свойст­во в нашем случае, можно написать:

 

 

Связь  с числами  Фибоначчи

 

Последовательностью Фибоначчи на­зывается последовательность, первые два члена которой равны 1, а каждый последующий — сумме двух преды­дущих. Таким образом, эта последо­вательность (обозначим ее через {un}) определяется  следующим образом:

u1 = 1, u2 = 1, un+2 = un+1 + un

(n = 1,2,3, ...).

 

Вот первые члены этой последова­тельности: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .

Вспомнив о приближениях числа  τ  подходящими дробями, мы заметим, что отношение любого члена последо­вательности Фибоначчи к последую­щему члену является подходящей дробью числа τ , то есть приближенным значением отношения золотого сече­ния. Это приближение тем лучше, чем больше номер взятого члена.

Если же взять три последователь­ных члена: un, un+1, un+2, то числа

 и

 

являются соседними подходящими дробями числа  τ, причём одна из этих дробей больше  τ, а дру­гая меньше.

Наконец, поставим следующий вопрос: как разделить целое число а на две целые части так, чтобы их от­ношение равнялось τ?

Так как  τ — иррациональное чис­ло, то такое деление, конечно, невоз­можно, интересующее нас отношение может лишь приближённо равняться  τ. Каково же это приближение? От­вет на этот вопрос даёт теория цепных дробей.

Пусть знаменатель подходящей дроби τ есть а. Рассмотрим множест­во всех дробей со знаменателями, не большими а. Оказывается, из мно­жества этих дробей ближе всех к числу  τ  находится именно  τ.

Но знаменатели подходящих дро­бей являются членами последователь­ности Фибоначчи, поэтому если а — член последовательности Фибоначчи, то деление а с помощью τ  будет хорошим приближением золотого се­чения.

Таким образом, разделить золотым сечением на две целые части с хорошим приближением можно числа, являю­щиеся членами последовательности Фибоначчи. Например, золотое сече­ние числа 8 дает (3,5), числа 13 — (5,8) и т. д.