Книга IV
Трёхбуквенная диаграмма

• Глава I  Символы и клетки
• Глава II  Представление суждений в терминах x и m или y и m
•   § 1. Представление суждений существования в терминах x и m или y и m
•   § 2. Представление суждений отношения в терминах x и m или y и m
• Глава III  Одновременное представление на одной диаграмме двух суждений отношения: одного в терминах x и m, другого — в терминах y и m
• Глава IV  Интерпретация трехбуквенной диаграммы с расставленными на ней фишками или цифрами в терминах x и y

Глава I
СИМВОЛЫ И КЛЕТКИ

Во-первых, условимся считать, что ниже слева изображена та самая двухбуквенная диаграмма, которой мы уже неоднократно пользовались в книге III. Начертим на ней внутренний квадрат и превратим ее в трехбуквенную диаграмму. Каждая из четырех клеток исходной (двухбуквенной) диаграммы разобьется при этом на две части, поэтому трехбуквенная диаграмма всего будет содержать 8 клеток. Такая диаграмма показана справа.

xy	xy'
x'y	x'y'

xym'			xy'm'
	xym	xy'm
	x'ym	x'y'm
x'ym'			x'y'm'

Во-вторых, предположим, что мы выбрали некоторый признак или совокупность признаков (то есть то, что ранее мы называли особенностью) m и разбили xy-класс на два подкласса с видовыми отличиями m и m'. Для одного из подклассов (который мы будем называть «классом xym-предметов», или «xym-классом») отведем внутреннюю северо-западную клетку, для другого (который мы будем называть «классом xym'-предметов», или «xym'-классом») — внешнюю северо-западную клетку («уголок»). Так, в примере с книгами мы могли бы выбрать в качестве m признак «переплетенные». Тогда m' означал бы признак «непереплетенные», и класс «старые английские книги» оказался бы разбитым на два подкласса: «старые английские переплетенные книги» и «старые английские непереплетенные книги». Одному из подклассов (xym) мы отвели бы внутреннюю северо-западную клетку, другому — (xym') — внешнюю.

В-третьих, предположим, что мы произвели аналогичное разбиение над xy', x'y и x'y'-классами и в каждом случае внутреннюю клетку сопоставили с тем классом, который обладает признаком m, а внешнюю — с тем классом, который обладает признаком m'. В примере с книгами мы подразделили бы класс «новые английские книги» на два подкласса: «новые английские переплетенные книги» и «новые английские непереплетенные книги». Первому из них мы сопоставили бы внутреннюю юго-западную, а второму — внешнюю юго-западную клетки. Вполне очевидно, что при таком соответствии между клетками и признаками внутренний квадрат отвечает m-классу, а окаймляющая его внешняя полоса — m'-классу. В примере с книгами внутренний квадрат соответствует «переплетенным книгам», внешняя полоса — «непереплетенным книгам».

Ознакомившись с трехбуквенной диаграммой, читатель должен научиться мгновенно отыскивать ту ее часть, которая отвечает любой наперед заданной паре признаков, или ту ее клетку, которая соответствует любому конкретному набору из трех признаков. Полезно придерживаться пи этом следующих правил.

1. Расположить признаки в порядке x, y, m.
2. Взять первый из упорядоченных признаков и отыскать ту часть трехбуквенной диаграммы, которая ему соответствует.
3. Затем взять второй признак и найти ту часть уже найденной (в п.2) части, которая соответствует ему.
4. Поступить аналогично с третьим признаком, если таковой имеется.

Предположим, что требуется найти часть диаграммы, соответствующую признаку ym. Мы говорим себе: «Признаком y обладает западная половина, а признаком m  — внутренняя часть западной половины диаграммы».

Еще один пример. Предположим, что требуется найти клетку, обладающею признаком x'ym'. Мы говорим себе: «Признаком x' обладает южная половина диаграммы, признаком y — западная часть южной половины, то есть юго-западная четверть диаграммы, а признаком m' — внешняя часть юго-западной четверти».

ТАБЛИЦА IV
Признак класса	Часть диаграммы или клетка, соответствующая признаку
x	Северная половина
x'	Южная половина
y	Западная половина
y'	Восточная половина
m	Внутренний квадрат
m'	Внешняя полоса
xy	Северо-западная четверть
xy'	Северо-восточная четверть
x'y	Юго-западная четверть
x'y'	Юго-восточная четверть
xm	Внутренняя часть северной половины
xm'	Внешняя часть северной половины
x'm	Внутренняя часть южной половины
x'm'	Внешняя часть южной половины
ym	Внутренняя часть западной половины
ym'	Внешняя часть западной половины
y'm	Внутренняя часть восточной половины
y'm'	Внешняя часть восточной половины
xym	Внутренняя часть северо-западной четверти
xym'	Внешняя часть северо-западной четверти
xy'm	Внутренняя часть северо-восточной четверти
xy'm'	Внешняя часть северо-восточной четверти
x'ym	Внутренняя часть юго-западной четверти
x'ym'	Внешняя часть юго-западной четверти
x'y'm	Внутренняя часть юго-восточной четверти
x'y'm'	Внешняя часть юго-восточной четверти

Читателю придется обратиться к своему гениальному другу и попросить, чтобы тот снова выступил в роли экзаменатора и погонял его по таблице IV.

Экзамен должен протекать в духе следующего диалога.

Вопрос. Каким признаком обладает внутренняя часть южной половины диаграммы?
Ответ. x'm.
Вопрос. Какая часть диаграммы отвечает признаку m?
Ответ. Внешняя полоса.
Вопрос. Каким признаком обладает внешняя часть северо-восточной четверти диаграммы?
Ответ. xy'm'.
Вопрос. Какая часть таблицы обладает признаком ym?
Ответ. Внутренняя часть западной половины.
Вопрос. Каким признаком обладает южная половина диаграммы?
Ответ. x'.
Вопрос. Какая клетка обладает признаком x'y'm?
Ответ. Внутренняя часть юго-восточной четверти.
И т.д. и т.п.

 

Глава II
ПРЕДСТАВЛЕНИЕ СУЖДЕНИЙ В ТЕРМИНАХ x И m ИЛИ y И m

§ 1. Представление суждений существования в терминах x и m или y и m

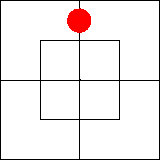
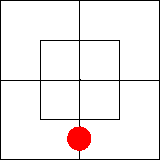
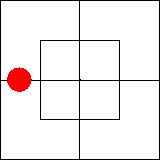
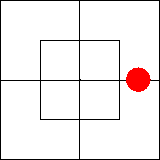
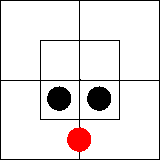
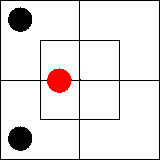
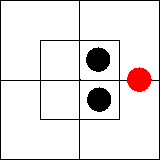
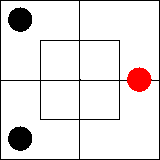
Начнем с суждения «Некоторые xm существуют». Напомним, что в развернутом виде, как уже объяснялось, это суждение формулируется так: «Некоторые реально существующие предметы суть xm-предметы». В нем утверждается, что во внутренней части северной половины имеется по крайней мере один предмет, то есть что эта часть диаграммы занята. Подобную ситуацию мы изобразим, поставив красную фишку на границу между клетками, образующими занятую часть диаграммы:



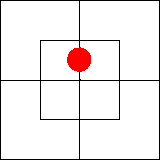
В примере с книгами соответствующее суждение означало бы: «Некоторые старые переплетенные книги существуют» или «Некоторые старые переплетенные книги есть (на самом деле)».

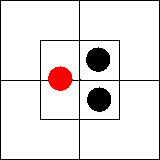
Аналогичным образом можно изобразить на диаграмме и семь других суждений того же типа: «Некоторые xm' существуют», «Некоторые x'm существуют», «Некоторые x'm' существуют», «Некоторые ym существуют», «Некоторые ym' существуют» , «Некоторые y'm существуют» , «Некоторые y'm' существуют».

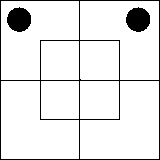
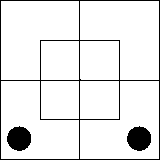
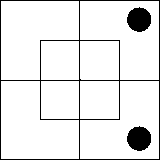
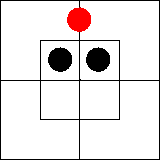
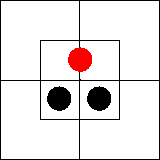
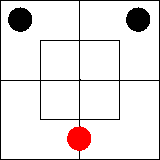
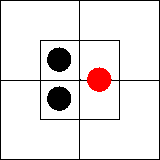
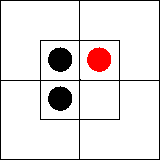
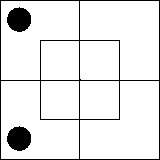
Рассмотрим далее суждение «Ни один xm не существует». В нем утверждается, что во внутренней части северной половины ничего нет или что эта часть диаграммы пуста. Такую ситуацию мы изобразим, поставив на внутреннюю часть северной половины диаграммы две черные фишки — по одной на каждую клетку:



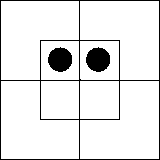
Шестнадцать суждений существования (названные и семь других того же типа) — вот все, что нам понадобится изображать на диаграмме.

 

§ 2. Представление суждений отношения в терминах x и m или y и m

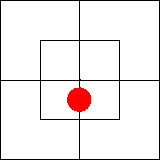
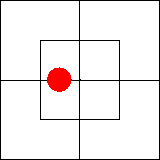
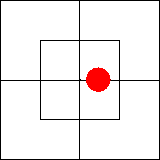
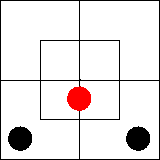
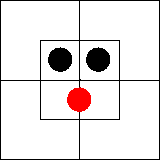
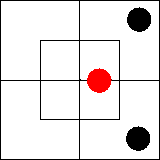
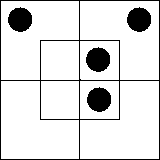
Начнем с двух суждений: «Некоторые x суть m» = «Некоторые m суть x». Известно, что каждое из них эквивалентно суждению существования «Некоторые xm существуют». Как изобразить его на диаграмме, мы уже знаем:



То же в терминах x и m или y и m можно сказать и о семи аналогичных парах суждений.

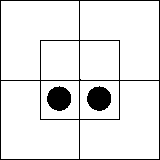
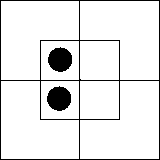
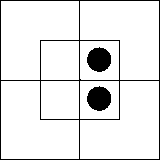
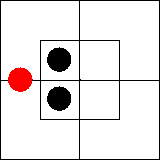
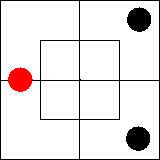
Рассмотрим, далее, пару обратных суждений: «Ни один x не есть m» = «Ни один m не есть x». Каждое из них эквивалентно суждению существования «Ни один xm не существует», которое мы уже умеем изображать на диаграмме.



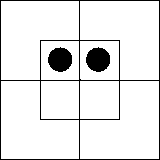
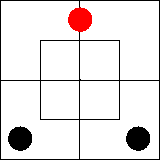
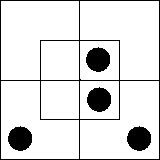
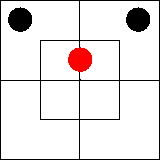
Рассмотрим теперь суждение «Все x суть m». Известно, (см. раньше), что это — двойное суждение и что оно эквивалентно двум суждениям: «некоторые x суть m» и «Ни один x не есть m'», каждое из которых мы уже умеем изображать на диаграмме.



Суждения отношения перечисленного выше типа (всего их 32) — единственные, которые мы должны уметь изображать на нашей диаграмме.

И снова вам придется обратиться у своему гениальному другу и попросить, чтобы он проэкзаменовал вас по таблицам V, VI, VII, VIII.

На столе перед «жертвой» не должно быть ничего, кроме чистой (незаполненной) трехбуквенной диаграммы, одной красной и двух черных фишек. С их помощью жертва должна изображать на диаграмме различные суждения, которые будет называть «инквизитор», например «Ни один y' не есть m», «Некоторые xm' существуют» и т.д. и т.п.

ТАБЛИЦА V Некоторые xm существуют = Некоторые x суть m = Некоторые m суть x Ни один xm не существует = Ни один x не есть m = Ни один m не есть x Некоторые xm' существуют = Некоторые x суть m' = Некоторые m' суть x Ни один xm' не существует = Ни один x не есть m' = Ни один m' не есть x Некоторые x'm существуют = Некоторые x' суть m = Некоторые m суть x' Ни один x'm не существует = Ни один x' не есть m = Ни один m не есть x' Некоторые x'm' существуют = Некоторые x' суть m' = Некоторые m' суть x' Ни один x'm' не существует = Ни один x' не есть m' = Ни один m' не есть x' ТАБЛИЦА VI Некоторые ym существуют = Некоторые y суть m = Некоторые m суть y Ни один ym не существует = Ни один y не есть m = Ни один m не есть y Некоторые ym' существуют = Некоторые y суть m' = Некоторые m' суть y Ни один ym' не существует = Ни один y не есть m' = Ни один m' не есть y Некоторые y'm существуют = Некоторые y' суть m = Некоторые m суть y' Ни один y'm не существует = Ни один y' не есть m = Ни один m не есть y' Некоторые y'm' существуют = Некоторые y' суть m' = Некоторые m' суть y' Ни один y'm' не существует = Ни один y' не есть m' = Ни один m' не есть y' ТАБЛИЦА VII Все x суть m Все x суть m' Все x' суть m Все x' суть m' Все m суть x Все m суть x' Все m' суть x Все m' суть x' ТАБЛИЦА VIII Все y суть m Все y суть m' Все y' суть m Все y' суть m' Все m суть y Все m суть y' Все m' суть y Все m' суть y'   Глава III ОДНОВРЕМЕННОЕ ПРЕДСТАВЛЕНИЕ НА ОДНОЙ ДИАГРАММЕ ДВУХ СУЖДЕНИЙ ОТНОШЕНИЯ: ОДНОГО В ТЕРМИНАХ x И m, ДРУГОГО — В ТЕРМИНАХ y И m Читателю рекомендуется не расставлять фишки на диаграмме, а вычерчивать для себя маленькие диаграммки и ставить в соответствующих клетках цифры 1 и 0. Единица будет означать красную фишку, иначе говоря, суждение «Здесь имеется по край ней мере один предмет», а нуль — черную, иначе говоря, суждение «Здесь ничего нет». ( Мы же на своих диаграммах по-прежнему будем пользоваться красными и черными фишками.) Одно из двух суждений, которые мы будем изображать на диаграмме, всегда будет в терминах x и m, а другое — в терминах y и m. Если какое-нибудь из суждений начинается со слова «все», то его необходимо предварительно разбить на два эквивалентных ему суждения. Если же на одной и той же диаграмме требуется представить два суждения, из которых одно начинается со слова «некоторые», а другое — со слов «ни один», то первым следует изобразить отрицательное суждение. Иногда это позволит нам избежать такого положения, когда единицу сначала приходится «усаживать на стенку», а затем сдвигать в одну из клеток. Разберем несколько примеров. I Ни один x не есть m'. Ни один y' не есть m. Представим сначала на диаграмме суждение «Ни один x не есть m'». У нас получится диаграмма a. Представив на ней суждение «Ни один y' не есть m», получим диаграмму b. a b II Некоторые m суть x. Ни один m не суть y. Если бы мы, пренебрегая правилами, начали с суждения «Некоторые m суть x», то у нас получилась бы диаграмма a. Взяв затем суждение «Ни один m не есть y», утверждающее, что внутренняя северо-западная клетка пуста, мы должны были бы снять единицу со стенки (поскольку выбор между двумя клетками произведен) и поставить ее во внутреннюю северо-восточную клетку, как показано на диаграмме с. Начав с суждения «Ни одно m не есть y», мы избавимся от всех этих хлопот (см. диаграмму b). Взяв затем суждение «Некоторые m суть x», нам уже нет необходимости усаживать единицу на стенку: единица сразу же отправляется в северо-восточную клетку, как на диаграмме с. a b c III Ни один x' не есть m'. Все m суть y. Прежде всего необходимо разбить второе суждение на два других суждения, которым оно эквивалентно. Таким образом, мы получаем три суждения: Ни один x' не есть m', Некоторые m суть y, Ни один m не есть y', которые необходимо представить на диаграмме. Рассмотрим их по порядку одно за другим. Начнем с суждения 1 — «Ни один x' не есть m'». Оно отвечает диаграмме a. Представив на ней суждение 3, а именно «Ни одно m не есть y'», получим диаграмму b. На этот раз единице, соответствующей суждению 2 («Некоторые m суть y»), не остается ничего другого, как сидеть на стенке, ибо у нас нет нуля, который мог бы заставить ее слезть оттуда! В результате мы получаем диаграмму с. a b c IV Все m суть x. Все y суть m. Разбив оба суждения в соответствии с правилами, мы получим четыре суждения, которые требуется представить на диаграмме: Некоторые m суть x, Ни одно m не есть x', Некоторые y суть m, Ни одно y не есть m'. Рассмотрим их в последовательности 2, 4, 1, 3. Взяв суждение 2 («Ни один m не есть x'»), получим диаграмму a. Представив на ней суждение 4 («Ни один y не есть m'»), получим диаграмму b. Взяв затем суждение 1 («Некоторые m суть x»), мы должны были бы посадить единицу на стенку. Поэтому мы берем вместо суждения 1 суждение 3 («Некоторые y суть m») и получаем диаграмму с. После этого необходимость в суждении 1 вообще отпадает, поскольку, посадив единицу на стенку, мы не узнаем ничего нового. Диаграмма c уже говорит нам, что «Некоторые m суть x». a b c   Глава IV ИНТЕРПРЕТАЦИЯ ТРЕХБУКВЕННОЙ ДИАГРАММЫ С РАССТАВЛЕННЫМИ НА НЕЙ ФИШКАМИ ИЛИ ЦИФРАМИ В ТЕРМИНАХ x И y Пусть задана трехбуквенная диаграмма с расставленными на ней фишками или нулями и единицами. Требуется узнать, какое суждение отношения в терминах x и y представлено на ней. Для начинающего лучше всего начертить рядом с трехбуквенной диаграммой двухбуквенную и попытаться перенести на нее все сведения, которые он только сможет извлечь из трехбуквенной диаграммы. Прочесть искомые суждения по двухбуквенной диаграмме уже не составит для него труда. Немного попрактиковавшись, он научится обходиться и без двухбуквенной диаграммы и читать готовый ответ прямо по исходной трехбуквенной диаграмме. Чтобы перенести информацию с трехбуквенной диаграммы на двухбуквенную, необходимо соблюдать следующие правила: Исследовать «содержимое» северо-западной четверти трехбуквенной диаграммы. Если эта четверть содержит единицу хотя бы в одной из клеток, то она, несомненно, считается занятой, и вы можете поставить единицу в северо-западной клетке двухбуквенной диаграммы. Если же эта четверть содержит два нуля — по одному в каждой из своих клеток, то она заведомо пуста, и в северо-западную клетку двухбуквенной диаграммы вы можете поставить нуль. Аналогичные операции необходимо проделать с северо-восточной, юго-западной и юго-восточной четвертями трехбуквенной диаграммы. Рассмотрим в качестве примеров трехбуквенные диаграммы, полученные в четырех примерах предыдущей главы. I В северо-западной четверти лишь одна из двух клеток пуста (помечена черной фишкой), поэтому мы не знаем, пуста или занята северо-западная клетка двухбуквенной диаграммы и, следовательно, не можем поставит в нее ни нуля, ни единицы. В северо-восточной четверти трехбуквенной диаграммы мы обнаруживаем два нуля. Поэтому эта четверть заведомо пуста. Так мы и пометим на двухбуквенной диаграмме. В юго-западной четверти вообще нет никаких цифр — ни нулей, ни единиц. В юго-восточной четверти стоит один нуль, но этого недостаточно, чтобы можно было сказать что-нибудь определенной о юго-восточной клетке двухбуквенной диаграммы. Итак, окончательный результат гласит: «Ни один x не есть y», или «Ни один y не есть x» (как вам больше нравится). II Информация, содержащаяся в северо-западной четверти, недостаточна для каких-либо выводов о северо-западной клетке двухбуквенной диаграммы. В северо-восточной четверти мы обнаруживаем единицу. Этот означает, что четверть занята. Следовательно, в северо-восточную клетку двухбуквенной диаграммы мы можем вписать единицу: Информация в юго-западной четверти слишком скудна, чтобы ею можно было воспользоваться. В юго-восточной четверти никакой информации вообще не содержится. Следовательно, в итоге мы получаем суждение, которое можно прочитать двояким способом: и как «Некоторые x суть y'», и как «Некоторые y' суть x». III Относительно северо-западной четверти мы не располагаем никакой информацией. (Единица, «сидящая на стенке», не может ничем нам помочь до тех пор, пока мы не узнаем, по какую сторону она намеревается спрыгнуть!) Информация относительно северо-восточной четверти диаграммы недостаточна, чтобы ею можно было воспользоваться. То же можно сказать и относительно юго-западной четверти. Юго-восточная четверть — единственная, из которой мы может извлечь нужную информацию: она заведомо пуста. На двухбуквенной диаграмме мы с уверенностью можем отметить, что и ее юго-восточная клетка пуста. В результате мы получаем суждение: либо «Ни один x' не есть y'», либо «Ни один y' не есть x'». Каким из них воспользоваться — дело вкуса. IV Северо-западная четверть этой диаграммы занята, несмотря на нуль, стоящий в ее внешней части. Поэтому в северо-западную клетку двухбуквенной диаграммы мы впишем единицу: Относительно северо-восточной четверти мы не располагаем никакими сведениями. Юго-западная четверть заведомо пуста, поэтому в юго-западную клетку двухбуквенной диаграммы мы впишем нуль: Относительно юго-восточной четверти сведений недостаточно. Результат можно сформулировать в виде суждения: «Все y суть x».