Книга V
Силлогизмы
- Глава I Введение
- Глава
II Задачи на силлогизмы
- §
1. Предварительные замечания
- §
2. Задачи первого типа
- §
3. Задачи второго типа
Глава
I
ВВЕДЕНИЕ
Говорят, что три двухбуквенных суждения образуют силлогизм, если:
- все шесть их терминов
являются видами, принадлежащими к одному и тому же роду;
- любые два из суждений
содержат два ко-класса (определение дано в главе III
книги I) относительно разбиения по какому-то из признаков;
- все три суждения
связаны между собой так, что если бы два первых суждения были истинными,
то и третье суждение было бы истинным.
Род, видом которого является каждый из шести
терминов, называется «Вселенной рассмотрения», или
просто «Вселенной». Первые два суждения называются посылками, третье — заключением.
Пары терминов, отвечающих ко-классам в разбиении по какому-то признаку и
входящих в посылки, называются исключаемыми;
остальные пары терминов называются оставляемыми.
О заключении силлогизма принято говорить, что оно
следует из посылок. Перед ним обычно ставят слово «следовательно» или отделяют
его от посылок горизонтальной чертой.
Исключаемыми термины названы потому, что их исключают,
и они не входят в заключение силлогизма. Оставляемыми термины названы потому,
что их оставляют, и они входят в заключение.
Необходимо иметь в виду, что ответ на вопрос,
будет ли данное заключение следовать из посылок, не зависит от
истинности или ложности того или иного суждения, входящего в силлогизм, а
определяется исключительно взаимосвязью между суждениями.
Рассмотрим, например, силлогизм:
Ни один x-предмет не есть m-предмет;
Ни один y-предмет не есть m'-предмет.
Ни один x-предмет не есть y-предмет.
Как мы уже знаем (см.
главу 3 книги III), его можно записать в следующем виде:
Ни один x не есть m;
Ни один y не есть m'.
Ни один x не есть y.
Первое и второе суждения содержат ко-классы m
и m', первое и третье — x и x' и, наконец, втрое и третье
— ко-классы y и y'. Таким образом, эти суждения связаны между
собой так (в этом мы убедимся позже), что если бы первые два из них были
истинными, то и третье суждение также было бы истинным.
Следовательно, эти три суждения образуют силлогизм.
Два суждения — «Ни один x не есть m» и «Ни один y не есть m'»
служат посылками силлогизма, суждение «Ни один x не есть y»
— его заключением. Исключаемыми являются термины m и m',
оставляемыми — термины x и y.
Итак, три исходных суждения можно записать в виде
силлогизма:
Ни один x не есть m;
Ни один y не есть m'.
Ни один x не есть y.
В качестве второго примера рассмотрим трио
суждений:
Все кошки знают французский язык.
Некоторые цыплята — кошки.
Некоторые цыплята знают
французский язык.
Если эти суждения записать в нормальной форме, то
они примут следующий вид:
Все кошки — существа, знающие
французский язык.
Некоторые цыплята — кошки.
Некоторые цыплята — существа,
знающие французский язык.
Все шесть терминов в этом случае являются видами,
принадлежащими к роду «существ».
Первое и второе суждения содержат ко-классы
«кошки» и «кошки», первое и третье — ко-классы «существа, понимающие французский
язык» и «существа, понимающие французский язык», и, наконец, второе и третье
суждения — ко-классы «цыплята» и «цыплята». Следовательно (это будет доказано далее),
эти три суждения связаны между собой так, что если бы первые два из них были
истинными, то и третье суждение было бы истинным. (По случайному стечению
обстоятельств первые два суждения на нашей планете, строго говоря, не
являются истинными. Однако ничто не мешает им быть истинными на какой-нибудь другой
планете, например, на Марсе или Юпитере. Там, же где истинны
первые два суждения, истинно и третье. Обитатели такой планеты вполне могли бы
нанимать цыплят в гувернеры и извлекать из этого (между прочим) еще одну
выгоду, неизвестную в Англии: всякий раз, когда в доме иссякнет запас провизии,
обед можно было бы готовить из гувернера!)
Итак, рассматриваемые нами три суждения образуют силлогизм.
Род «существ» служит его «Вселенной», два суждения «Все кошки знают французский
язык» и «Некоторые цыплята — кошки» — его посылками, суждение «Некоторые
цыплята знают французский язык» — заключением. Исключаемыми
являются термины «кошки» и «кошки», оставляемыми — термины «существа, знающие
французский язык» и «цыплята».
Таким образом, исходные три суждения можно
записать так:
Все кошки знают французский язык,
Некоторые цыплята — кошки.
Некоторые цыплята знают
французский язык.
Глава II
ЗАДАЧИ НА СИЛЛОГИЗМЫ
§
1. Предварительные замечания
Если термины суждения выражены словами, то
суждение называется конкретным. Если же
термины суждения выражены буквами, то суждение называется абстрактным. Чтобы преобразовать суждения из
конкретной формы в абстрактную, мы фиксируем Вселенную, рассматриваем
каждый термин как один из ее видов и выбираем буквенное обозначение для видового
отличия, присущего этому виду.
Пусть, например, требуется привести к абстрактной
форме суждение «Некоторые солдаты храбрые». В качестве Вселенной мы можем
выбрать множество людей, а «солдат» и «храбрых людей» рассматривать как виды,
принадлежащие роду «людей». Пусть x означает отличительный признак
(например, «военные») «солдаты», а y — «храбрые». Тогда суждение можно
записать в следующем виде: «Некоторые военные люди — храбрые люди», то есть как
суждение «Некоторые x-люди суть y-люди», или, опуская слово
«люди» (по этому поводу см. объяснения в главе 3 книги III),
как «Некоторые x суть y».
Мы не будем каждый раз проделывать все операции
столь подробно и обычно, указав Вселенную («люди») и значения «x-солдаты»
и «y-храбрые», будем сразу же заменять конкретное суждение «Некоторые
солдаты храбрые» абстрактным суждением «Некоторые x суть y».
Задачи, которые мы будем решать, делятся на два
типа.
- Даны два суждения
отношения, содержащие два ко-класса. Требуется установить, какое
заключение следует из этих суждений, если принять их за посылки
силлогизма.
- Даны три суждения
отношения, из которых любые два содержат по два ко-класса. Предположив,
что эти суждения образуют силлогизм, проверить, следует ли третье суждение
из первых двух и если следует, то является ли заключение полным.
Рассмотрим каждый из этих типов задач в
отдельности.
§ 2. Задачи первого типа
Вывод заключения из двух суждений отношения,
содержащих два ко-класса
и принимаемых за посылки силлогизма
Правила решения таких задач сводятся к следующему:
- Определить вселенную.
- Составить словарь так,
чтобы m ( или m' ) отвечали одной паре ко-классов,
а x ( или x' ) и y ( или y' )
— двум другим парам ко-классов.
- Записать приведенные в
условии задачи посылки в абстрактной форме.
- Представить обе
посылки на одной трехбуквенной диаграмме.
- Проверить, какое еще
суждение (если таковое вообще существует) в терминах x и y
представлено на диаграмме.
- Записать это суждение
в конкретной форме.
Ясно, если посылки, сформулированные в условии
задачи, были бы истинными, то и обнаруженное на диаграмме суждение также
было бы истинным. Поэтому его можно считать заключением, следующим из
данных посылок. Рассмотрим несколько примеров.
I
Ни один мой сын не мошенник.
К честному человеку люди всегда
относятся с уважением.
Выбрав «людей» в качестве Вселенной, приведем эти
два суждения к следующему виду:
Ни один мой сын не мошенник
(нечестный человек).
Всех честных людей уважают (другие
люди).
Составим наш словарик: пусть m =
честные, x = мои сыновья, y = пользующиеся уважением.
(Обратите внимание на то, что выражение «x = мои сыновья» служит
сокращенной формой выражения «x = видовому отличию „моих сыновей“,
рассматриваемых как вид, принадлежащий роду „люди“»).
Теперь мы должны представить оба суждения в
абстрактной форме:
Ни один x не есть m'.
Все m суть y.
Пользуясь приемами, описанными в главе 3 книги
IV представим эти суждения на трехбуквенной диаграмме.
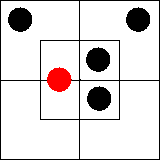
Теперь, следуя правилам, изложенным в главе 4 книги
IV, перенесем всю информацию, которую мы только сможем извлечь из
трехбуквенной диаграммы, на двухбуквенную диаграмму:

Полученный результат можно сформулировать и как
«Ни один x не есть y'», и как «Ни один y' не есть x»
(обе формы одинаково допустимы). Обращаясь к словарику, выберем ту из них,
которая звучит лучше. Предположим, что мы остановили свой выбор на суждении «Ни
один x не есть y'». В конкретной форме оно будет звучать так:
Ни к одному из моих сыновей
никто никогда не относится без уважения.
Все кошки знают французский
язык.
Некоторые цыплята — кошки.
Выбрав «живые существа» в качестве Вселенной,
запишем суждения в виде:
Все кошки — живые существа,
знающие французский язык.
некоторые цыплята — кошки.
Теперь мы уже можем составить словарик: m =
кошки, x = знающие французский язык, y = цыплята.
В абстрактной форме наши суждения будут выглядеть
так:
Все m суть x.
Некоторые y суть m'.
Чтобы представить их на трехбуквенной диаграмме,
разобьем первое из суждений на два суждения, которым оно эквивалентно, и
получим три суждения:
- Некоторые m
суть x.
- Ни одно m не
есть x'.
- Некоторые y
суть m.
Согласно правилам, приведенным в главе 3 книги
IV эти суждения следует наносить на диаграмму в таком порядке: 2, 1,
3.
Проделав все необходимые операции, мы получили бы следующий
результат:
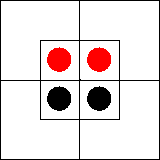
Поэтому наносить суждения на диаграмму удобнее в
другом порядке, а именно 2, 3, 1. Представив на диаграмме суждения 2 и 3 мы
получим
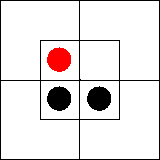
Относительно суждения 1 можно вообще не беспокоиться,
поскольку суждение «Некоторые m суть x» уже представлено на
диаграмме. Перенеся все сведения на двухбуквенную диаграмму, мы увидим
следующую картину:

Полученный результат можно сформулировать и как
«Некоторые x суть y», и как «Некоторые y суть x».
Справившись в словаре, остановим свой выбор на
суждении «Некоторые y суть x», или , в конкретной форме, Некоторые цыплята знают французский язык.
III
Все, кто предстал перед судом
на его прошлой выездной сессии и был признан виновным, приговорены к
заключению.
Некоторые из тех, кто был
приговорен к заключению, были также приговорены к каторжным работам.
Пусть Вселенной будут «те, кто предстал перед
судом на его прошлой выездной сессии», m = приговоренные к
заключению, x = признанные виновными, y = приговоренные
к каторжным работам. Тогда исходные посылки, записанные в абстрактной форме,
будут иметь вид:
Все x суть m.
Некоторые m суть y.
Разобьем первое суждение на два:
- Некоторые x
суть m.
- Ни один x не
есть m'.
- Некоторые m
суть y.
Нанесем их на трехбуквенную диаграмму в
последовательности 2,1,3 и получим следующий результат:
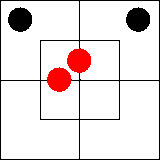
В этом случае мы не можем вывести никакого
заключения. Глядя на одни лишь посылки, вы могли бы подумать, что
заключением должно быть суждение «Некоторые из тех, кого признали виновным,
приговорены к каторжным работам». Но такое заключение неверно, если
говорить о той выездной сессии суда, которую я придумал.
— Как неверно! — воскликните вы. — А кого же
приговорили к заключению и к каторжным работам, как не тех, кто был признан
виновным? Иначе как их можно было вообще осудить?
Тем не менее все произошло именно так, как я
сказал. Было три разбойника с большой дороги, совершивших ограбление. Представ
перед судом, они сразу же признали себя виновными. Присяжным не пришлось
выносить вердикта, поскольку виновность преступников не вызывала сомнений.
А теперь я еще раз кратко повторю уже
рассмотренные три задачи, но в форме, которой надлежит следовать при
самостоятельном решении других задач.
I
Ни один мой сын не мошенник.
К честному человеку люди всегда
относятся с уважением.
Вселенная — «люди», m =честные, x =
мои сыновья, y = пользующиеся уважением.
Ни один x не есть m'.
Все m суть y.


Следовательно, «Ни один x не есть y'»,
или
Ни к одному из моих сыновей
никто никогда не относится без уважения.
II
Все кошки знают французский
язык.
Некоторые цыплята — кошки.
Вселенная — «живые существа», m =
кошки, x = знающие французский язык, y = цыплята.
Все m суть x.
Некоторые y суть m.


Следовательно, «Некоторые y суть x»,
то есть
Некоторые цыплята знают
французский язык.
III
Все, кто предстал перед судом
на его прошлой выездной сессии и был признан виновным, приговорены к
заключению.
Некоторые из тех, кто был
приговорен к заключению, были также приговорены к каторжным работам.
Вселенная — «те, кто предстал перед судом на его
прошлой выездной сессии», m = приговоренные к заключению, x =
признанные виновными, y = приговоренные к каторжным работам.
Все x суть m.
Некоторые m суть y.

Заключения нет.
§ 3. Задачи второго типа
Проверка правильности и полноты заключения силлогизма,
образованного тремя суждениями отношения,
из которых любые два содержат по два ко-класса.
Правила решения таких задач сводятся к следующему:
- С помощью метода,
изложенного в §2 главы II книги V найти заключение (если таковое
существует), следующее из посылок, входящих в условие задачи.
- Если из посылок
никакого заключения не следует, сказать об этом.
- Если из посылок в
условии задачи заключение следует, то сравнить его с заключением,
приведенным в условии задачи, и сделать соответствующий вывод.
В качестве образца, которому читатель должен
следовать при самостоятельном решении задач, я приведу в кратчайшей форме
решение шести задач.
I
Все солдаты сильные.
Все солдаты храбрые.
Некоторые сильные люди храбры.
Вселенная — «люди», m = солдаты, x =
сильные, y = храбрые.
Все m суть x.
Все m суть y.
Некоторые x суть y.
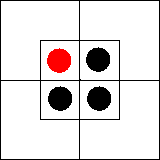

Следовательно, «Некоторые x суть y».
Заключение в условии задачи правильно.
II
Я восхищен этими картинами.
Когда я что-нибудь меня
восхищает, мне хочется разглядеть это «что-нибудь» особенно внимательно.
Некоторые из этих картин я хочу
разглядеть особенно внимательно.
Вселенная — «предметы», m = то, что
восхищает меня, x = эти картины, y = предметы, которые
я хочу разглядеть особенно внимательно.
Все x суть m.
Все m суть y.
Некоторые x суть y.
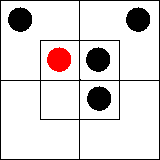

Следовательно, «Все x суть y».
Таким образом, сформулированное в условии задачи
заключение неполно. Полное заключение имеет форму суждения «Все
эти картины я хочу разглядеть особенно внимательно».
III
Лишь тот, кто храбр, достоин
славы.
Некоторые хвастуны — трусы.
Некоторые хвастуны недостойны
славы.
Вселенная — «люди», m = храбрые, x =
достойные славы, y = хвастуны.
Ни один m' не есть x.
Некоторые y суть m'.
Некоторые y суть x'.
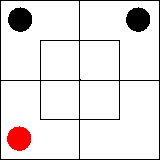

Следовательно, «Некоторые y суть x'».
Таким образом, заключение, приведенное в условии
задачи, правильно.
IV
Все солдаты умеют маршировать.
Некоторые маленькие дети — не
солдаты.
Некоторые маленькие дети не
умеют маршировать.
Вселенная — «люди», m =солдаты, x =
умеющие маршировать, y = маленькие дети.
Все m суть x.
Некоторые y суть m'.
Некоторые y суть x'.
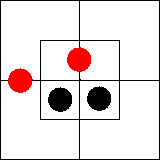
Заключения нет.
V
Все эгоистичные люди неприятны
окружающим.
Все обязательные люди приятны
окружающим.
Все обязательные люди
неэгоистичны.
Вселенная — «люди», m = приятные
окружающим, x = эгоистичные, y = обязательные.
Все x суть m'.
Все y суть m.
Все y суть x'.
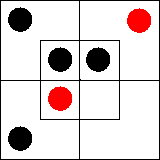

Следовательно, «Все x суть y' и Все y
суть x'».
Таким образом, заключение в условии задачи неполно.
Полное заключение содержит еще одно суждение: «Все эгоистичные люди
необязательны».
Никому из тех, кто хочет ехать
поездом, кто не может достать экипаж и кто не имеет времени, чтобы спокойно
дойти до станции, не миновать пробежки.
Эти туристы намереваются ехать
поездом, но не могут достать экипаж, зато у них достаточно времени, чтобы
спокойно дойти до станции.
Этим туристам не придется
бежать.
Вселенная — «те, кто хочет ехать поездом и не
может достать экипаж», m = имеющие достаточно времени, чтобы
спокойно дойти до станции, x = те, кому нужно бежать, y =
эти туристы.
Ни одно m' не есть x'.
Все y суть m.
Все y суть x'.
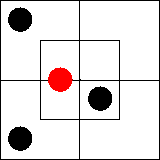
Заключения нет.
Вот еще один удобный случай, любезный
читатель, чтобы разыграть твоего невинного друга. Предложите ему силлогизм,
сформулированный в условии задачи, и спросите, что он думает о заключении.
Скорее всего он ответит:
— Оно абсолютно правильно! А если твоя драгоценная
книга утверждает, будто оно неправильно, не верь ей! Ведь не думаешь же ты, что
этим туристам придется бежать, чтобы успеть на поезд? Если бы я был
одним из них и знал, что посылки истинны, то мне было бы совершенно
ясно, что бежать не придется, и я бы преспокойно отправился на станцию
пешком!
На это вы должны возразить:
— А если за тобой погонится бешеный бык?
В ответ на такое замечание ваш друг скажет
примерно следующее:
— Гм! Минуточку! Я подумаю.
И тут настанет удобный момент для того, чтобы
разъяснить ему удобный способ проверки правильности силлогизма: если можно
придумать обстоятельства, которые, не влияя на истинность посылок,
сделают заключение ложным, то силлогизм неправилен.